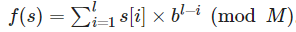字符串哈希

参考：
OI-WIKI-# 字符串哈希
宫水三叶-# 字符串哈希入门
Leetcode-187重复的 DNA 序列

性质

具体来说，哈希函数最重要的性质可以概括为下面两条：

1. 在 Hash 函数值不一样的时候，两个字符串一定不一样；

2. 在 Hash 函数值一样的时候，两个字符串不一定一样（哈希冲突/碰撞。但大概率一样，且我们当然希望它们总是一样的）。

哈希函数

我们需要关注的是什么？

时间复杂度和 Hash 的准确率。

通常我们采用的是多项式 Hash的方法，对于一个长度为 L 的字符串 s 来说，我们可以这样定义多项式 Hash 函数：

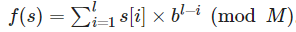
这种情况下，对于字符串 xyz ，其哈希函数值为 xb^2 + yb + z。

对于该 Hash 函数的参考实现如下(（效率低下的版本，实际使用时一般不会这么写）)

using std::string;

const int M = 1e9 + 7; 
const int B = 233; 

typedef long long ll; 


int get_hash(const string& s) { 
	int res = 0; 
	for (int i = 0; i < s.size(); ++i) { 
		res = (ll)(res * B + s[i]) % M; 
	} 
	return res; 
} 

bool cmp(const string& s, const string& t) { 
	return get_hash(s) == get_hash(t); 
}

多次询问子串哈希

单次计算一个字符串的哈希值复杂度是 O(n)，其中 n 为串长，与暴力匹配没有区别，如果需要多次询问一个字符串的子串的哈希值，每次重新计算效率会非常低下。

一般采取的方法是对整个字符串先 预处理出每个前缀的哈希值(设该数组为H) ，将哈希值看成一个 b 进制的数对 m 取模的结果，这样的话可以做到快速求出子串的哈希。

首先对于F(s[1, i]) ，即原串长度为 i 的前缀（即子串s[1, i]）的哈希值 (即H[i]) ，按照定义为

F(s[1, i])  = s[1] * b^ (i - 1) + s[2] * b ^ (i - 2) + … + s[i - 1] * b +s[i]

现在，我们想要用类似前缀和的方式快速求出子串 s[L, R] 的哈希值即 F(s[L, R])，按照定义哈希值为

F(s[L, R])  = s[L] * b^ (R - L) + s[L + 1] * b ^ (R - L - 1) + … + s[R - 1] * b +s[R]

对比观察上述两个式子，可以发现 式2 其实可以由 式1 得出，即
F(s[L, R])  = F(s[1, R]) - F(s[1, L-1]) * b ^ (r - L + 1)

那么即字串 S[L, R] 的哈希值等于 H[R] - H[L-1] * B ^ (R - L +1)

而 B ^ (r - L + 1)  又可以通过 O(n) 的预处理出次方数组，以实现 O(1) 的回答每次询问

例题，LC-1044-最长重复子串 :

class Solution {
    public String longestDupSubstring(String s) {
        int n = s.length();
        StringHash stringHash = new StringHash(s);
        int left = 1;
        int right = n + 1;
        int start = -1;
        while (left < right) {
            int mid = left + (right - left >> 1);
            boolean check = false;
            Set<Long> seen = new HashSet<>();
            for (int i = 0; i < n && i + mid - 1 < n; i++) {
                long hash = stringHash.get(i, i + mid - 1);
                if (!seen.add(hash)) {
                    check = true;
                    start = i;
                    break;
                }
            }
            if (check) {
                left = mid + 1;
            }else{
                right = mid;
            }
        }
        return start == -1 ? "" : s.substring(start, start + left - 1);
    }
}

class StringHash {
    private static final int B = 131313;
    private static final int STR_MAX_LENGTH = (int)3e4;
    private static final long[] POWER = new long[STR_MAX_LENGTH + 1];
    private final long[] hashTable;

    static {
        POWER[0] = 1;
        for(int i = 1; i < STR_MAX_LENGTH + 1; i++){
            POWER[i] = POWER[i - 1] * B;
        }
    }

    public StringHash(String s) {
        hashTable = new long[s.length() + 1];
        for(int i = 1; i <= s.length(); i++){
            hashTable[i] = hashTable[i - 1] * B + s.charAt(i - 1);
        }
    }

    // [i, j]
    public long get(int i, int j) {
        // h(r) - h(l - 1) * b ^ (r - l + 1)
        return hashTable[j + 1] - hashTable[i - 1 + 1] * POWER[j - i + 1];
    }
}