题目描述
leetcode 中等题
给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 queries 。
请你找出一个长度为 n 的 二维 答案数组 answer ,其中 answer[i] = [mini, maxi] :
mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值,则使用 -1 代替。
maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值,则使用 -1 代替。
返回数组 answer 。
示例1:
1
2
3
4
5
6
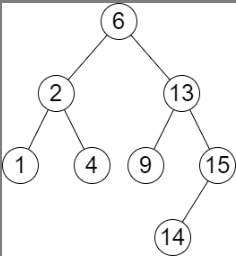
| 输入:root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出:[[2,2],[4,6],[15,-1]]
解释:按下面的描述找出并返回查询的答案:
- 树中小于等于 2 的最大值是 2 ,且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ,且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ,且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。
|
提示1:
1
2
3
4
5
| 树中节点的数目在范围 [2, 105] 内
1 <= Node.val <= 106
n == queries.length
1 <= n <= 105
1 <= queries[i] <= 106
|
二分查找
需要注意的是题目给的是二叉查找树而不是平衡树,如果直接在树上查找的话,某些数据下树可能会退化成链表导致 TLE。
中序遍历树得到排序后的数组,再二分查找出 $min_x$ 以及 $max_x$ 即可。
可以通过两次左闭右开的二分查找分别通过缩小右边界、左边界获得 $min_x$ 和 $max_x$ 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Solution {
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
List<Integer> sort = dfs(root, new ArrayList<>());
int n = sort.size();
List<List<Integer>> ans = new ArrayList<>();
for(int i = 0; i < queries.size(); i++){
List<Integer> cur = new ArrayList<>();
int left = 0, right = n, target = queries.get(i);
while(left < right){
int mid = left + (right - left >> 1);
if(sort.get(mid) < target){
left = mid + 1;
}else if(sort.get(mid) >= target){
right = mid;
}
}
if(left < n && sort.get(left) == target){
cur.add(sort.get(left));
}else if(left - 1 >= 0){
cur.add(sort.get(left - 1));
}else{
cur.add(-1);
}
left = 0;
right = n;
while(left < right){
int mid = left + (right - left >> 1);
if(sort.get(mid) <= target){
left = mid + 1;
}else if(sort.get(mid) > target){
right = mid;
}
}
if(left - 1 >= 0 && sort.get(left - 1) == target){
cur.add(sort.get(left - 1));
}else if(left < n){
cur.add(sort.get(left));
}else{
cur.add(-1);
}
ans.add(cur);
}
return ans;
}
private List<Integer> dfs(TreeNode root, List<Integer> sort){
if(root == null){
return sort;
}
dfs(root.left, sort);
sort.add(root.val);
dfs(root.right, sort);
return sort;
}
}
|
当然也可以通过缩小右边界一次性得到 $min_x$ 和 $max_x$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
List<Integer> sort = dfs(root, new ArrayList());
int n = sort.size();
List<List<Integer>> ans = new ArrayList<>();
for(int i = 0; i < queries.size(); i++){
List<Integer> cur = new ArrayList<>();
int left = 0, right = n, target = queries.get(i);
while(left < right){
int mid = left + (right - left >> 1);
if(sort.get(mid) < target){
left = mid + 1;
}else{
right = mid;
}
}
if(left < n && sort.get(left) == target){
cur.add(sort.get(left));
}else if(left - 1 >= 0){
cur.add(sort.get(left - 1));
}else{
cur.add(-1);
}
int b = (left < n ? sort.get(left) : -1);
cur.add(b);
ans.add(cur);
}
return ans;
}
private List<Integer> dfs(TreeNode root, List<Integer> sort){
if(root == null){
return sort;
}
dfs(root.left, sort);
sort.add(root.val);
dfs(root.right, sort);
return sort;
}
}
|
缩小左边界一次性得到 $min_x$ 和 $max_x$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
List<Integer> sort = dfs(root, new ArrayList());
int n = sort.size();
List<List<Integer>> ans = new ArrayList<>();
for(int i = 0; i < queries.size(); i++){
List<Integer> cur = new ArrayList<>();
int left = 0, right = n, target = queries.get(i);
while(left < right){
int mid = left + (right - left >> 1);
if(sort.get(mid) > target){
right = mid;
}else{
left = mid + 1;
}
}
int a = (left - 1 >= 0 ? sort.get(left - 1) : -1);
cur.add(a);
if(left - 1 >= 0 && sort.get(left - 1) == target){
cur.add(sort.get(left - 1));
}else if(left < n){
cur.add(sort.get(left));
}else{
cur.add(-1);
}
ans.add(cur);
}
return ans;
}
private List<Integer> dfs(TreeNode root, List<Integer> sort){
if(root == null){
return sort;
}
dfs(root.left, sort);
sort.add(root.val);
dfs(root.right, sort);
return sort;
}
}
|
