题目描述
leetcode 中等题
给你一个 n 个点的无向图,节点从 0 到 n - 1 编号。给你一个长度为 n 下标从 0 开始的整数数组 vals ,其中 vals[i] 表示第 i 个节点的值。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条双向边。
星图 是给定图中的一个子图,它包含一个中心节点和 0 个或更多个邻居。换言之,星图是给定图中一个边的子集,且这些边都有一个公共节点。
下图分别展示了有 3 个和 4 个邻居的星图,蓝色节点为中心节点。
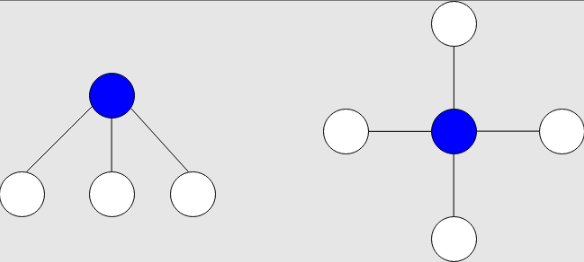
星和 定义为星图中所有节点值的和。
给你一个整数 k ,请你返回 至多 包含 k 条边的星图中的 最大星和 。
示例1:
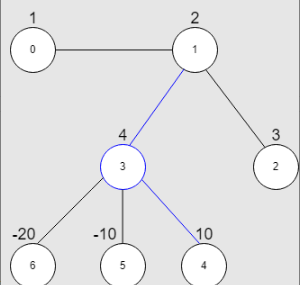
1
2
3
4
5
| 输入:vals = , edges = , k = 2
输出:16
解释:上图展示了输入示例。
最大星和对应的星图在上图中用蓝色标出。中心节点是 3 ,星图中还包含邻居 1 和 4 。
无法得到一个和大于 16 且边数不超过 2 的星图。
|
提示1:
1
2
3
4
5
6
7
8
| n == vals.length
1 <= n <= 10^5
-10^4 <= vals[i] <= 10^4
0 <= edges.length <= min(n * (n - 1) / 2, 10^5)
edges[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
0 <= k <= n - 1
|
排序 + 暴力枚举
注意题目中:星图是给定图中一个边的子集,且这些边都有一个公共节点。
所以我们可以直接暴力枚举所有中心点,并根据 $vals$ 中的值对该点上的边进行排序,从而找出所有点中的最大值即可。
当然由于 $val$ 可能为负数,且题目为“至多包含k条边”,所以当权值出现负数时,该点就不需要继续往下添加边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public int maxStarSum(int[] vals, int[][] edges, int k) {
int n = vals.length;
List<Integer>[] g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
for(int i = 0; i < edges.length; i++){
g[edges[i][0]].add(vals[edges[i][1]]);
g[edges[i][1]].add(vals[edges[i][0]]);
}
int ans = vals[0];
for(int i = 0; i < n; i++){
int cur = vals[i];
Collections.sort(g[i]);
for(int j = g[i].size() - 1; j >= 0 && j > g[i].size() - 1 - k; j--){
if(g[i].get(j) <= 0){
break;
}
cur += g[i].get(j);
}
ans = Math.max(ans, cur);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public int maxStarSum(int[] vals, int[][] edges, int k) {
int n = vals.length;
PriorityQueue<Integer>[] g = new PriorityQueue[n];
Arrays.setAll(g, i -> new PriorityQueue<Integer>((a, b) -> b - a));
for(int i = 0; i < edges.length; i++){
g[edges[i][0]].offer(vals[edges[i][1]]);
g[edges[i][1]].offer(vals[edges[i][0]]);
}
int ans = vals[0];
for(int i = 0; i < n; i++){
int cur = vals[i];
int count = 0;
while(!g[i].isEmpty() && count < k){
if(g[i].peek() <= 0){
break;
}
cur += g[i].poll();
count++;
}
ans = Math.max(ans, cur);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public int maxStarSum(int[] vals, int[][] edges, int k) {
HashMap<Integer, PriorityQueue<Integer>> map = new HashMap<>();
for (int[] edge : edges) {
map.computeIfAbsent(edge[0], t -> new PriorityQueue<>()).offer(-vals[edge[1]]);
map.computeIfAbsent(edge[1], t -> new PriorityQueue<>()).offer(-vals[edge[0]]);
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < vals.length; i++) {
for (int j = 0; j < k && map.containsKey(i) && !map.get(i).isEmpty() && map.get(i).peek() < 0; j++) {
vals[i] -= map.get(i).poll();
}
max = Math.max(max, vals[i]);
}
return max;
}
}
|

