题目描述
leetcode 中等题
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
找出 左上角 为 (row1i, col1i) 且 右下角 为 (row2i, col2i) 的子矩阵,将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1i <= x <= row2i 和 col1i <= y <= col2i 的 mat[x][y] 加 1 。
返回执行完所有操作后得到的矩阵 mat 。
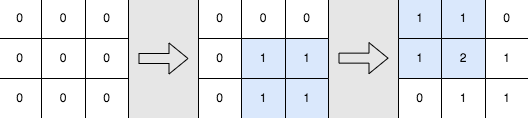
示例1:
1
2
3
4
5
| 输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出:[[1,1,0],[1,2,1],[0,1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
|
提示1:
1
2
3
4
| 1 <= n <= 500
1 <= queries.length <= 10^4
0 <= row1i <= row2i < n
0 <= col1i <= col2i < n
|
多次一维差分
暴力解法的时间复杂度为 $O(n^2 \times queries.length)$ , 上限为 $500 \times 500 \times 10^4 \approx 10 ^ 9$,显然会 TLE 。
一种做法是通过多次的一维 差分 来加速对矩阵某行的加一,此时的时间复杂度为 $O(n \times queries.length + n^2)$ ,上限为 $500 \times 10 ^4 \approx 10^6$ ,符合要求。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] a = new int[n][n];
for(int[] item : queries){
for(int i = item[0]; i <= item[2]; i++){
a[i][item[1]]++;
if(item[3] + 1 < n){
a[i][item[3] + 1]--;
}
}
}
for(int i = 0; i < n; i++){
for(int j = 1; j < n; j++){
a[i][j] += a[i][j - 1];
}
}
return a;
}
}
|
二维差分
一种更优的做法是 二维差分。
为了方便,初始化差分数组大小为 $[n + 2][n + 2]$,其中一次加 $1$ 是为了避免特判差分修正时的下标溢出;另一次加 $1$ 是为了避免特判做 二维前缀和 时下标为负数的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] diff = new int[n + 2][n + 2];
for(int[] item : queries){
a[item[0] + 1][item[1] + 1]++;
a[item[0] + 1][item[3] + 2]--;
a[item[2] + 2][item[1] + 1]--;
a[item[2] + 2][item[3] + 2]++;
}
int[][] ans = new int[n][n];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
ans[i - 1][j - 1] = a[i][j];
}
}
return ans;
}
}
|
