题目描述
leetcode 中等题
给你一个下标从 0 开始的 m x n 二进制 矩阵 grid 。你可以从一个格子 (row, col) 移动到格子 (row + 1, col) 或者 (row, col + 1) ,前提是前往的格子值为 1 。如果从 (0, 0) 到 (m - 1, n - 1) 没有任何路径,我们称该矩阵是 不连通 的。
你可以翻转 最多一个 格子的值(也可以不翻转)。你 不能翻转 格子 (0, 0) 和 (m - 1, n - 1) 。
如果可以使矩阵不连通,请你返回 true ,否则返回 false 。
注意 ,翻转一个格子的值,可以使它的值从 0 变 1 ,或从 1 变 0 。
示例1:
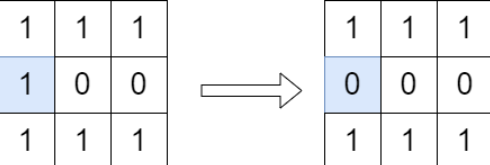
1
2
3
| 输入:grid = [[1,1,1],[1,0,0],[1,1,1]]
输出:true
解释:按照上图所示我们翻转蓝色格子里的值,翻转后从 (0, 0) 到 (2, 2) 没有路径。
|
提示1:
1
2
3
4
5
| m == grid.length
n == grid[i].length
1 <= m, n <= 1000
1 <= m * n <= 10^5
grid[0][0] == grid[m - 1][n - 1] == 1
|
遍历轮廓
下轮廓:优先向下走,否则再向右走
右轮廓:优先向右走,否则再向下走
一个结论是:如果两个轮廓有交集(除了起点终点),那么翻转交集中的任意一个格子,都可以使矩阵不连通。
实际代码中,可以在遍历某个轮廓时,直接将该轮廓的所有点翻转,那么假设第二次出发还能到达终点,则无法使矩阵不连通。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
int m;
int n;
public boolean isPossibleToCutPath(int[][] grid) {
m = grid.length;
n = grid[0].length;
if(!clean(grid, 0, 0)){
return true;
}
Queue<int[]> queue = new ArrayDeque<>();
queue.offer(new int[]{0, 0});
int cnt = 0;
while(!queue.isEmpty()){
int[] index = queue.poll();
if(index[0] == m - 1 && index[1] == n - 1){
return false;
}
if(index[0] + 1 < m && grid[index[0] + 1][index[1]] == 1){
grid[index[0] + 1][index[1]] = 0;
queue.offer(new int[]{index[0] + 1, index[1]});
}
if(index[1] + 1 < n && grid[index[0]][index[1] + 1] == 1){
grid[index[0]][index[1] + 1] = 0;
queue.offer(new int[]{index[0], index[1] + 1});
}
}
return true;
}
private boolean clean(int[][] grid, int x, int y){
if(y == m - 1 && x == n - 1){
return true;
}
grid[y][x] = 0;
if(x + 1 < n && grid[y][x + 1] == 1){
return clean(grid, x + 1, y);
}
if(y + 1 < m && grid[y + 1][x] == 1){
return clean(grid, x, y + 1);
}
return false;
}
}
|
注意到可以通过一个通用的 $dfs$ 来满足两次遍历的需求,还可以用 $逻辑与$ 来实现优先某个方向的逻辑。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
int[][] grid;
int m;
int n;
public boolean isPossibleToCutPath(int[][] grid) {
this.grid = grid;
m = grid.length;
n = grid[0].length;
return !dfs(0, 0) || !dfs(0, 0);
}
private boolean dfs(int x, int y){
if(y == m - 1 && x == n - 1){
return true;
}
grid[y][x] = 0;
return (x + 1 < n && grid[y][x + 1] == 1 && dfs(x + 1, y)) ||
(y + 1 < m && grid[y + 1][x] == 1 && dfs(x, y + 1));
}
}
|
