题目描述
leetcode 困难题
给你一个正整数 n ,表示一个 无向 图中的节点数目,节点编号从 1 到 n 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 双向 边。注意给定的图可能是不连通的。
请你将图划分为 m 个组(编号从 1 开始),满足以下要求:
- 图中每个节点都只属于一个组。
- 图中每条边连接的两个点 [ai, bi] ,如果 ai 属于编号为 x 的组,bi 属于编号为 y 的组,那么 |y - x| = 1 。
请你返回最多可以将节点分为多少个组(也就是最大的 m )。如果没办法在给定条件下分组,请你返回 -1 。
示例1:
1
2
3
4
5
6
7
8
9
| 输入:n = 6, edges =
输出:4
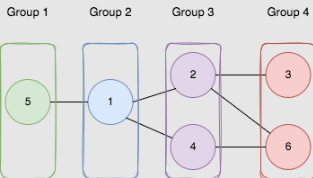
解释:如上图所示,
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组,将第三个组或者第四个组中任何一个节点放到第五个组,至少有一条边连接的两个节点所属的组编号不符合题目要求。
|
提示1:
1
2
3
4
5
6
| 1 <= n <= 500
1 <= edges.length <= 10^4
edges[i].length == 2
1 <= ai, bi <= n
ai != bi
两个点之间至多只有一条边。
|
二分图判定 + BFS
一个结论是如果一个图能够按照题意进行划分,必然是一个二分图。所以可以先跑一遍二分图判定,如果非二分图直接返回即可。
然后再考虑如何得出最大组数。先考虑连通块内的划分,题目中的划分要求其实等价于 $bfs$ 中同一层的节点需要划分到同一组,所以我们枚举每个点作为起点进行 $bfs$ ,$bfs$ 过程中的最大深度就为该连通块所能划分的最大组数。而为了让组数尽量多,我们让不同连通块之间划分到不同组,那么不同连通块能够划分的组数相加即为答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class Solution {
private List<Integer>[] g;
private int[] color;
public int magnificentSets(int n, int[][] edges) {
color = new int[n];
g = (List<Integer>[])(new List[n + 1]);
Arrays.setAll(g, i -> new ArrayList<>());
for(int[] e : edges){
g[e[0] - 1].add(e[1] - 1);
g[e[1] - 1].add(e[0] - 1);
}
int ans = 0;
for(int i = 0; i < n; i++){
if(color[i] != 0){
continue;
}
List<Integer> connect = new ArrayList<>();
if(!dfs(i, 1, connect)){
return -1;
}
ans += connect.stream().mapToInt(this::bfs).max().orElseThrow();
}
return ans;
}
private boolean dfs(int p, int curColor, List<Integer> connect){
connect.add(p);
color[p] = curColor;
for(int item : g[p]){
if((color[item] ^ curColor) == 0){
return false;
}
if(color[item] != 0){
continue;
}
if(!dfs(item, 3 ^ curColor, connect)){
return false;
}
}
return true;
}
private int bfs(int p){
int maxDepth = 0;
boolean[] visit = new boolean[color.length];
Deque<int[]> queue = new ArrayDeque<>();
queue.offer(new int[]{p, 1});
visit[p] = true;
while(!queue.isEmpty()){
int[] top = queue.poll();
maxDepth = Math.max(maxDepth, top[1]);
for(int item : g[top[0]]){
if(visit[item]){
continue;
}
visit[item] = true;
queue.offer(new int[]{item, top[1] + 1});
}
}
return maxDepth;
}
}
|
