题目描述
leetcode 困难题
给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
从树中 移除 以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不 等于根节点的值。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意:
- 查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
- 树的高度是从根到树中某个节点的 最长简单路径中的边数 。
示例1:
1
2
3
4
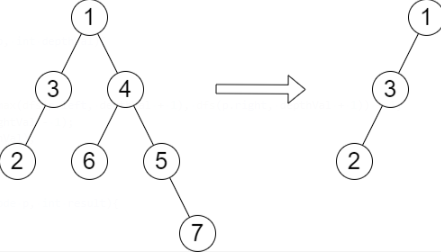
| 输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出:[2]
解释:上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2(路径为 1 -> 3 -> 2)。
|
提示1:
1
2
3
4
5
6
7
8
| 树中节点的数目是 n
2 <= n <= 10^5
1 <= Node.val <= n
树中的所有值 互不相同
m == queries.length
1 <= m <= min(n, 10^4)
1 <= queries[i] <= n
queries[i] != root.val
|
dfs
设当前节点为 $p$ ,以 $p.left$ 为例,询问结果为
$max(depth(p) + height(right), depth(p.father) + height(p.father.otherChild))$
其中 $depth(x)$ 为某个节点 $x$ 的深度, $height(x)$ 为以 $x$ 节点作为根节点的子树高度。表达式前者表示经过 $p$ 以及 $p.right$ 时的最大路径长度,后者为不经过 $p$ 时的最大路径长度,显然答案为两者的最大值。
具体可以通过两次 $dfs$ 来实现, 其中第一次 $dfs$ 预处理出 $height$ 和 $depth$ , 第二次 $dfs$ 处理出对于每个节点的询问答案。
时间复杂度 $O(n)$ ,$n$ 为节点个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import java.util.Optional;
class Solution {
private final Map<Integer, Integer> height = new HashMap<>();
private final Map<Integer, Integer> depth = new HashMap<>();
private final Map<Integer, Integer> ans = new HashMap<>();
public int[] treeQueries(TreeNode root, int[] queries) {
dfs(root, 0);
dfsAns(root, 0);
return Arrays.stream(queries).map(ans::get).toArray();
}
private int dfs(TreeNode p, int depthVal){
if(p == null){
return 0;
}
int heightVal = Math.max(dfs(p.left, depthVal + 1), dfs(p.right, depthVal + 1)) + 1;
height.put(p.val, heightVal - 1);
depth.put(p.val, depthVal);
return heightVal;
}
private void dfsAns(TreeNode p, int result){
if(p == null){
return;
}
ans.put(p.val, result);
dfsAns(p.left, Math.max(depth.get(p.val) +
height.getOrDefault(Optional.ofNullable(p.right).orElseGet(TreeNode::new).val, -1) + 1, result));
dfsAns(p.right, Math.max(depth.get(p.val) +
height.getOrDefault(Optional.ofNullable(p.left).orElseGet(TreeNode::new).val, -1) + 1, result));
}
}
|
