题目描述
leetcode 困难题
给你一棵 n 个节点的树(连通无向无环的图),节点编号从 0 到 n - 1 且恰好有 n - 1 条边。
给你一个长度为 n 下标从 0 开始的整数数组 vals ,分别表示每个节点的值。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
一条 好路径 需要满足以下条件:
开始节点和结束节点的值 相同 。
开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值(也就是说开始节点的值应该是路径上所有节点的最大值)。
请你返回不同好路径的数目。
注意,一条路径和它反向的路径算作 同一 路径。比方说, 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。
示例1:
1
2
3
4
5
6
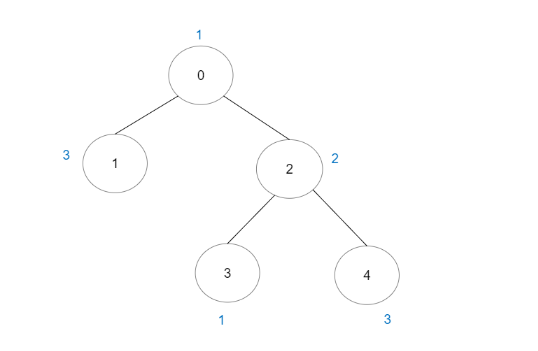
| 输入:vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
输出:6
解释:总共有 5 条单个节点的好路径。
还有 1 条好路径:1 -> 0 -> 2 -> 4 。
(反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径)
注意 0 -> 2 -> 3 不是一条好路径,因为 vals[2] > vals[0] 。
|
提示1:
1
2
3
4
5
6
7
8
| n == vals.length
1 <= n <= 3 * 10^4
0 <= vals[i] <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵合法的树。
|
并查集
我们考虑枚举任意等值两点 $a$ 、$b$ 作为好路径的端点时是否合法,按照题意如果它们的路径上所有点都小于 $vals[a]$ 时合法。
稍微将问题转化下,我们从小到大枚举这些等值点,从小到大将小于当前枚举到的点的边加入到树中,那么如果此时这些等值点已经连通,则说明它们之间路径必然不存在更大权值的点,为好路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| class Solution {
public int numberOfGoodPaths(int[] vals, int[][] edges) {
Arrays.sort(edges, Comparator.comparingInt(a -> Math.max(vals[a[0]], vals[a[1]])));
Map<Integer, List<Integer>> sortPoint = new TreeMap<>();
for (int i = 0; i < vals.length; i++) {
sortPoint.computeIfAbsent(vals[i], k -> new ArrayList<>())
.add(i);
}
UF uf = new UF(vals.length);
int ans = 0;
int eIndex = 0;
for (Map.Entry<Integer, List<Integer>> e : sortPoint.entrySet()) {
while (eIndex < edges.length && Math.max(vals[edges[eIndex][0]], vals[edges[eIndex][1]]) <= e.getKey()) {
uf.union(edges[eIndex][0], edges[eIndex][1]);
eIndex++;
}
Map<Integer, Integer> cnt = new HashMap<>();
for (int maxP : e.getValue()) {
int fa = uf.find(maxP);
ans += cnt.merge(fa, 1, Integer::sum);
}
}
return ans;
}
}
class UF{
int[] fa;
int[] size;
public UF(int n) {
fa = IntStream.range(0, n).toArray();
size = IntStream.generate(() -> 1).limit(n).toArray();
}
void union(int x, int y){
int fx = find(x);
int fy = find(y);
if (fx == fy) {
return;
}
if (size[fx] < size[fy]) {
fx ^= fy;
fy ^= fx;
fx ^= fy;
}
fa[fy] = fx;
size[fx] += size[fy];
}
int find(int a){
if (a != fa[a]) {
fa[a] = find(fa[a]);
}
return fa[a];
}
}
|
