LC-6378.最小化旅行的价格总和

题目描述

leetcode 困难题

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例1：

输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
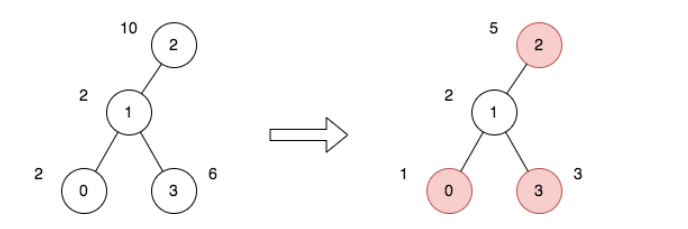
上图表示将节点 2 视为根之后的树结构。
第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

提示1：

1 <= n <= 50
edges.length == n - 1
0 <= ai, bi <= n - 1
edges 表示一棵有效的树
price.length == n
price[i] 是一个偶数
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= starti, endi <= n - 1

树形 DP

需要注意的是贪心解法是错的，也就是说价格减半的点并不止两种情况，可以参考打家劫舍或者以下这个例子

1000 -> 1 -> 1 -> 1000

最优的选择明显是将第一个和最后一个节点价格减半，而不是分奇偶节点。

没有陷入贪心解法的误区的话，其实问题就类似打家劫舍了。

不同的是我们需要求出每个节点的实际价格，而由于树上任意节点间的路径固定，所以我们只需要求出每个节点经过的次数，将该次数乘上原价格即可得出该节点的实际价格。

求每个节点的经过次数有两种做法：

暴力 DFS

注意到题目数据规模较小，可以暴力枚举所有旅行，将经过的点计数加一即可。

时间复杂度： $O(nq)$ ，$q$ 为旅行次数

class Solution {
    Map<Integer, List<Integer>> g = new HashMap<>();
    int[] cnt;
    int[] price;
    
    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        this.price = price;
        cnt = new int[n];
        for (int[] e : edges) {
            g.computeIfAbsent(e[1], __ -> new ArrayList<>())
                    .add(e[0]);
            g.computeIfAbsent(e[0], __ -> new ArrayList<>())
                    .add(e[1]);
        }
        Arrays.stream(trips).forEach(t -> tripCnt(t[0], t[1], -1));
        return Arrays.stream(dfs(0, -1)).min().orElseThrow();
    }

    private boolean tripCnt(int node, int end, int fa) {
        if (node == end) {
            cnt[end]++;
            return true;
        }
        for (int connect : g.getOrDefault(node, Collections.emptyList())) {
            if (connect == fa) {
                continue;
            }
            if (tripCnt(connect, end, node)) {
                cnt[node]++;
                return true;
            }
        }
        return false;
    }

    private int[] dfs(int node, int fa) {
        int val = cnt[node] * price[node];
        int[] ret = new int[]{val, val / 2};
        for (int connect : g.getOrDefault(node, Collections.emptyList())) {
            if (connect == fa) {
                continue;
            }
            int[] dp = dfs(connect, node);
            // 当前不减半，相邻取小
            ret[0] +=  Math.min(dp[0], dp[1]);
            // 当前减半，相邻必然不能减半
            ret[1] += dp[0]; 
        }
        return ret;
    }
}

Tarjan LCA + 树上差分

树上任意两个节点 $a、b$ 的路径等价于 $a -> lca(a, b) -> b$ ，维护 $cnt[i]$ 表示节点 $i$ 对其祖先节点的贡献，那么节点 $a$ 经过次数即为 $i$ 子树下所有 $cnt[i]$ 之和。

$cnt$ 的维护过程依赖差分，假设存在 $(a, b)$ 旅行，有:

• $cnt[a]$++
• $cnt[b]$++
• $cnt[lca]$–
• $cnt[fa[lca]]$–

总体更新完毕后，再自底向上更新差分值即可。

剩下问题为求旅行节点的 $lca$ ，可以通过 Tarjan 求出。

时间复杂度：$O(n + qlog(n))$ 。$n$ 和 $trip.length$ 出到 $1e5$ 时该解法同样适用。

class Solution {
    Map<Integer, List<Integer>> g = new HashMap<>();
    Map<Integer, List<int[]>> tripMap = new HashMap<>();
    Map<Integer, Integer> lcaMap = new HashMap<>();
    Map<Integer, Integer> faMap = new HashMap<>();
    int[] uf;
    int[] cnt;
    int[] price;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        this.price = price;
        cnt = new int[n];
        uf = IntStream.range(0, n).toArray();
        for (int[] e : edges) {
            g.computeIfAbsent(e[1], __ -> new ArrayList<>())
                    .add(e[0]);
            g.computeIfAbsent(e[0], __ -> new ArrayList<>())
                    .add(e[1]);
        }
        for (int i = 0; i < trips.length; i++) {
            tripMap.computeIfAbsent(trips[i][0], __ -> new ArrayList<>())
                    .add(new int[]{trips[i][1], i});
            tripMap.computeIfAbsent(trips[i][1], __ -> new ArrayList<>())
                    .add(new int[]{trips[i][0], i});
        }
        tarjanLca(0, -1, new HashSet<>());
        diffCnt(trips);
        return Arrays.stream(dfs(0, -1)).min().orElseThrow();
    }

    private void tarjanLca(int node, int fa, Set<Integer> visit) {
        faMap.put(node, fa);
        visit.add(node);
        for (int connect : g.getOrDefault(node, Collections.emptyList())) {
            if (connect == fa) {
                continue;
            }
            tarjanLca(connect, node, visit);
            uf[connect] = node;
        }
        for (int[] q : tripMap.getOrDefault(node, Collections.emptyList())) {
            if (!visit.contains(q[0])) {
                continue;
            }
            lcaMap.put(q[1], find(q[0]));
        }
    }

    private void diffCnt(int[][] trips) {
        for (int i = 0; i < trips.length; i++) {
            int[] t = trips[i];
            cnt[t[0]]++;
            cnt[t[1]]++;
            int lca = lcaMap.get(i);
            int lcaFa = faMap.getOrDefault(lca, -1);
            if (lcaFa != -1) {
                cnt[lcaFa]--;
            }
            cnt[lca]--;
        }
    }

    private int[] dfs(int node, int fa) {
        int[] ret = new int[]{0, 0};
        for (int connect : g.getOrDefault(node, Collections.emptyList())) {
            if (connect == fa) {
                continue;
            }
            int[] dp = dfs(connect, node);
            // 当前不减半，相邻取小
            ret[0] +=  Math.min(dp[0], dp[1]);
            // 当前减半，相邻必然不能减半
            ret[1] += dp[0];
            cnt[node] += cnt[connect];
        }
        int val = price[node] * cnt[node];
        ret[0] += val;
        ret[1] += val / 2;
        return ret;
    }

    private int find(int point) {
        if (point != uf[point]) {
            uf[point] = find(uf[point]);
        }
        return uf[point];
    }
}